前のページ　　　次のページ

第2章　固体微粒子間の点接触による化学結合

2.1　固体微粒子の近距離力による点接着

　　物質は万有引力の力で接着しているのではありません。万有引力は中和されずに遠方まで効果がおよびますが(式.3) に示すように、 原子レベルの距離においては万有引力(式.1) に対してクーロン力(式.2)は34桁も強いです。クーロン力は荷電粒子には作用しますが正負の電荷で打ち消し合うので 効果が及ぶのは原子レベルの程度の距離です。

　FG = G・(mp)²/d² ;　 G=6.67x10^-11 [N・m²・kg^-2],　m_p=1.66x10^-27 [kg] 　(1)

　　FC = k・(qp)²/d² ;　　 k=9.0x10⁹ [N・m²・C^-2], qp = 1.6x10^-19[C] 　　　(2)

　　　　FG / FC = 1.84x10^-64/(2.3x10^-28) = 8x10^-35. 　　　　　　　　 　　　　 (3)

　　他方、 宇宙塵の塊は微粒子の集団であり局部的な近距離力で構築されています。
水素や酸素などの遊離原子が共有結合を形成する反応のエネルギーは50～110 kcal/molです。 イオン結合のエネルギーは 3～7 kcal/molの範囲にあります。弱い結合であるファンデルワールス結合のエネルギーは1～2 kcal/mol です。 これに対して、25℃の熱運動のエネルギーは0.6 kcal/molです。そこで、宇宙空間で孤立分子が宇宙塵に 衝突しても多くの気体分子は跳ね返ります。ところが微粒子と微粒子が接触すると、原子と原子が原子の大きさ程度に接近する場所があり、原子の電子が他の原子の電子と相互に作用して、 高いエネルギー状態と低いエネルギー状態を発生し、エネルギーの低い状態ができます。 図1. に結合状態によって低下する一個当たりの原子のエネルギーを示します。
　
　　
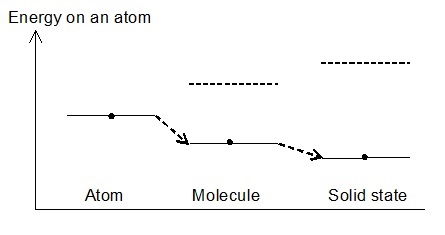
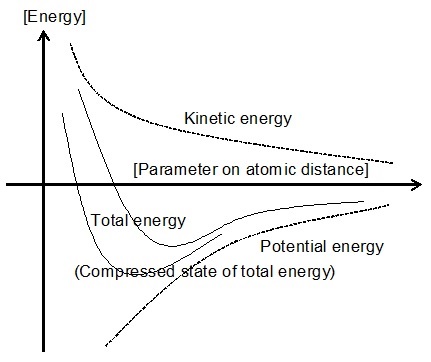
図1. 結合状態によって変化するネルギー状態　 　　　　　　　図2．原子間距離の縮小によるエネルギーの低下

　 図2.に 物質の量子状態を変えずに圧縮と膨張をした場合のエネルギー変化を示します。これはポテンシャルエネルギーと運動エネルギーの和が最も低くなる状態を与えるビリアル定理という平衡状態の条件を図示しています。ここで、運動量空間と距離空間の積を変えない条件が量子状態一定の条件になりますが、この条件によって、理想気体において圧力と体積の積を変えないと空間距離を圧縮した時に、運動エネルギーは反比例して増加します。 原子核と電子に働く引き合うポテンシャルエネルギーはサイズに反比例して減少ますが、 運動エネルギーはサイズの二乗に反比例して増加します。 そこで、最低のエネルギー状態は運動エネルギーがポテンシャルエネルギーの半分の状態で与えられます。(last modified Feb/26 2023)
　

目次　　　　　　　　　　　　　　　　　　　　-2.1-